In order to calculate, sangi or counting rods were used in the Edo priod.
Sangi were usually interpreted as follows:
Red rods stand for positive numbers and black negative ones.
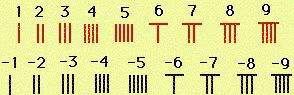 |
To solve the cubic equation -9 + 3x + 2x^2 + x^3 = 0, we arrange the sangi as fig.1. Sho, the top row, is reserved for the root, jitsu, the second row for the sangi representing the coefficient of the 0th power of the unknown quantity, ho, the third row for the coefficient of x, ren, the fourth row for the coefficient of x^2, gu, the fifth row for the coefficient of x^3, etc.
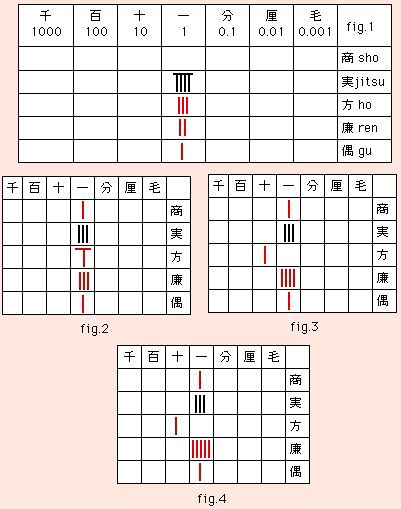 |
Putting 1 in sho we obtain fig.2.
sho1*gu1 + ren2 = 3 (which is again used in ren)
sho1*ren3 + ho3 = 6 (which is again used in ho)
sho1*ho6 + jistu(-9) = (-3) (which is again used in jitsu)
In fig.2, putting 1 in sho, we obtain fig.3.
sho1*gu1 + ren3 = 4 (which is again used in ren)
sho1*ren4 + ho6 = 10 (whic is again used in ho)
Similarly in fig.3, we have fig.4.
sho1*gu1 + ren4 = 5 (which is again used in ren in fig.4)
The operations illustrated here mean that we have obtained
-3 + 10y + 5y^2 + y^3 = 0,
after transforming x = y + 1 into -9 + 3x + 2x^2 + x^3 = 0.
So as to make the number in sho more exact, we transform y = z + 0.2
into the equation.
These transformations could be shown in Horner's scheme in comparison with figures.
fig.1 1) -9 3 2 1
6 3 1
-----------------------
fig.2 -3 6 3 1
.. 4 1
-----------------
fig.3 10 4 1
1
-------------
5 1
fig.4 -3 + 10y + 5y^2 + y^3 = 0